문제 소개
https://www.acmicpc.net/problem/16565

해결과정
접근 방법
완전 수학문제이다. 경우의 수를 구하는 문제이다. 포카드 4장을 뽑아야 이기는 경우의 수니까 만약 5장의 카드를 뽑는다면 무조건 포카드를 뽑아야 하므로 4장은 포카드, 나머지 1장을 (52장 - 4장)에서 고를 수 있는 경우의 수이다.
그렇다면 8장을 뽑는다면 어떻게 될까? 우선 이기려면 4장은 포카드 나머지 4장을 (52장 - 4장)에서 고르는 경우의 수가 있는데 여기서 하나를 더 고려해야 한다. 포카드를 2세트를 뽑았을 때는 경우의 수가 중복이 된다는 것을 알 수 있다. 왜냐하면 포카드 1세트를 고르고 나머지 4장으로 경우의 수를 돌렸는데 4장이 포카 들어가 나올 경우가 생긴다. 이 경우가 중복이 된다. 따라서 빼준다.
만약 12장을 뽑는다면? 1세트 뽑고 8장을 고르는 경우의 수에서 2세트 뽑고 4장을 고르는 경우의 수를 빼주는데, 3세트를 뽑는 경우의 수는 2세트를 뽑고 4장을 고르는 경우의 수에서 빼줘버렸다! 그래서 3세트를 뽑는 경우의 수는 다시 더해줘야 한다. 이것을 식으로 나타낸다면 아래와 같다. 이것을 코드로 구현하면 된다.

조합 경우의 수 구현
문제가 하나 더있다. 경우의 수를 10007로 나눈 나머지를 출력하라는 말이 있는데, 이 말을 곰곰이 생각해 보면 nCr를 계산했을 때 팩토리얼이 들어가기 때문에 값이 무지막지하게 커진다는 것을 알 수 있다. 재귀함수로 nCr을 구할 수 있지만 아래의 공식으로 구하면 좀 더 쉽게 구할 수 있을 것 같아 아래의 공식을 활용하여 nCr을 구했다.
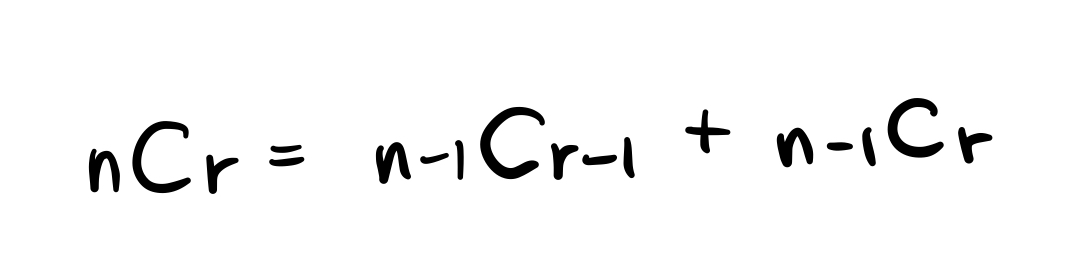
정답코드
모듈러 연산만 조심하면 된다. 왜냐하면 -1 의 i+1 제곱이 있기 때문에 나머지로만 계산하게 되면 음수가 될 수 있어서 이를 보정해줘야 한다.
import Foundation
let card = Int(readLine()!)!
let mod = 10007
var comb = Array(repeating: Array(repeating: 0, count: 53), count: 53)
for n in 0...52 {
comb[n][0] = 1
comb[n][n] = 1
}
for n in 1...52 {
for r in 1..<n {
comb[n][r] = (comb[n-1][r-1] + comb[n-1][r]) % mod
}
}
var ans = 0
var i = 1
while 4 * i <= card {
let k = (i % 2 == 1 ? 1 : -1)
ans = (ans + k * comb[13][i] * comb[52 - 4 * i][card - 4 * i]) % mod
if ans < 0 { ans += mod }
i += 1
}
print(ans)
'→ Problems' 카테고리의 다른 글
| [Algorithm] 백준 - 2098번 외판원 순회 (Swift) (0) | 2024.07.28 |
|---|---|
| [Algorithm] 백준 - 11689번 GCD(n, k) = 1 (0) | 2024.07.09 |
| [Algorithm] 백준 - 15824번 너 봄에는 캡사이신이 맛있단다 (Swift) (0) | 2024.07.07 |
| [Algorithm] 백준 - 1334번 철로 (Swift) (0) | 2024.07.07 |
| [Algorithm] 백준 - 1019번 책 페이지 (Swift) (0) | 2024.07.06 |