Segment Tree 란?
세그먼트 트리는 범위 데이터의 조회, 업데이트에 효과적인 자료구조이다. 이진트리의 형태로 바로 O(logN)의 시간복잡도를 가지게 된다. 가장 많이 쓰이는 것은 특정 범위 내의 요소들에 대한 합계, 최솟값, 최댓값을 검색하고 처리할 수 있다.
Segment Tree 만들기
만약 [1, 2, 3, 4, 5] 와 같은 배열이 있다고 해보자. 이것을 Segment Tree 자료에 넣어 합계를 쉽게 검색하고 싶다. 어떻게 해야 할까? 이진트리의 기본 개념처럼 계속 반으로 쪼개서 저장해 주면 된다.

하지만 우리가 원하는 것은 합계 뿐... 아래처럼 저장해 주면 Segment Tree 끝!이다. 참 쉽죠? 이것을 코드로 구현해 보자.
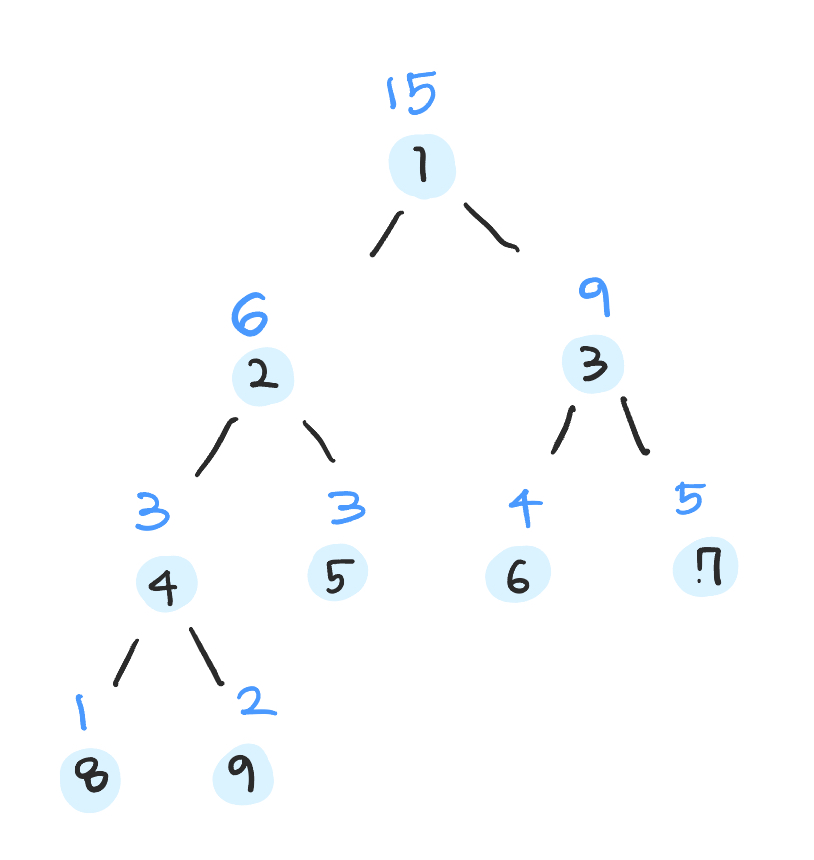
Segment Tree를 만들기 위한 고민
Tree의 크기는 어떻게 결정하죠?
아래의 공식이 있는데... 음 트리의 높이와 여러 가지를 고려하면 아래와 같이 정확히 크기를 지정해 줄 수 있지만 통상적으로 4N으로 여유롭게 잡는다고 한다.

합을 어떻게 구해줄까요? Segment Tree를 어떻게 만들까요?
재귀함수를 사용하면 된다. 트리의 구조를 살펴보면 자식노드들의 합이 부모노드인 것을 볼 수 있다. 이를 사용하여 아래와 같이 트리를 만들어 준다.
let nums = [1, 2, 3, 4, 5]
let N = nums.count
var tree = Array(repeating: 0, count: 4 * N) // 4N 으로 트리 크기 지정
@discardableResult
func makeSegmentTree(_ start: Int, _ end: Int, _ node: Int) -> Int {
if start == end {
tree[node] = nums[start] // 끝까지 왔다면 자기 자신
return tree[node]
}
let mid = (start + end) / 2 // 반으로 나누기 위한 mid
let leftChild = makeTree(start, mid, node * 2)
let rightChild = makeTree(mid + 1, end, node * 2 + 1)
tree[node] = leftChild + rightChild // 왼쪽 오른쪽 자식노드 더해주기
return tree[node]
}
makeSegmentTree(0, N-1, 1) // 편의를 위해 노드의 시작은 1부터 한다.
Segment Tree를 만들었는데 이것을 어떻게 활용할까?
위와 똑같은 그림에 index만 빨간 글씨로 적어놓았다. 여기서 [1, 2, 3, 4, 5]에서 2~4까지의 합을 구하고 싶다면 어떻게 구할까? 3~4까지의 합인 9와 2의 합인 3을 더해주면 12가 나온다. 물론 배열의 크기가 5라서 이게 뭐 하는 짓일까?라는 생각이 들겠지만 배열의 크기가 커지면 커질수록 Segment Tree는 진가를 발휘하게 될 것이다. 매번 합을 구해줄 필요 없이 검색만 해주면 된다!
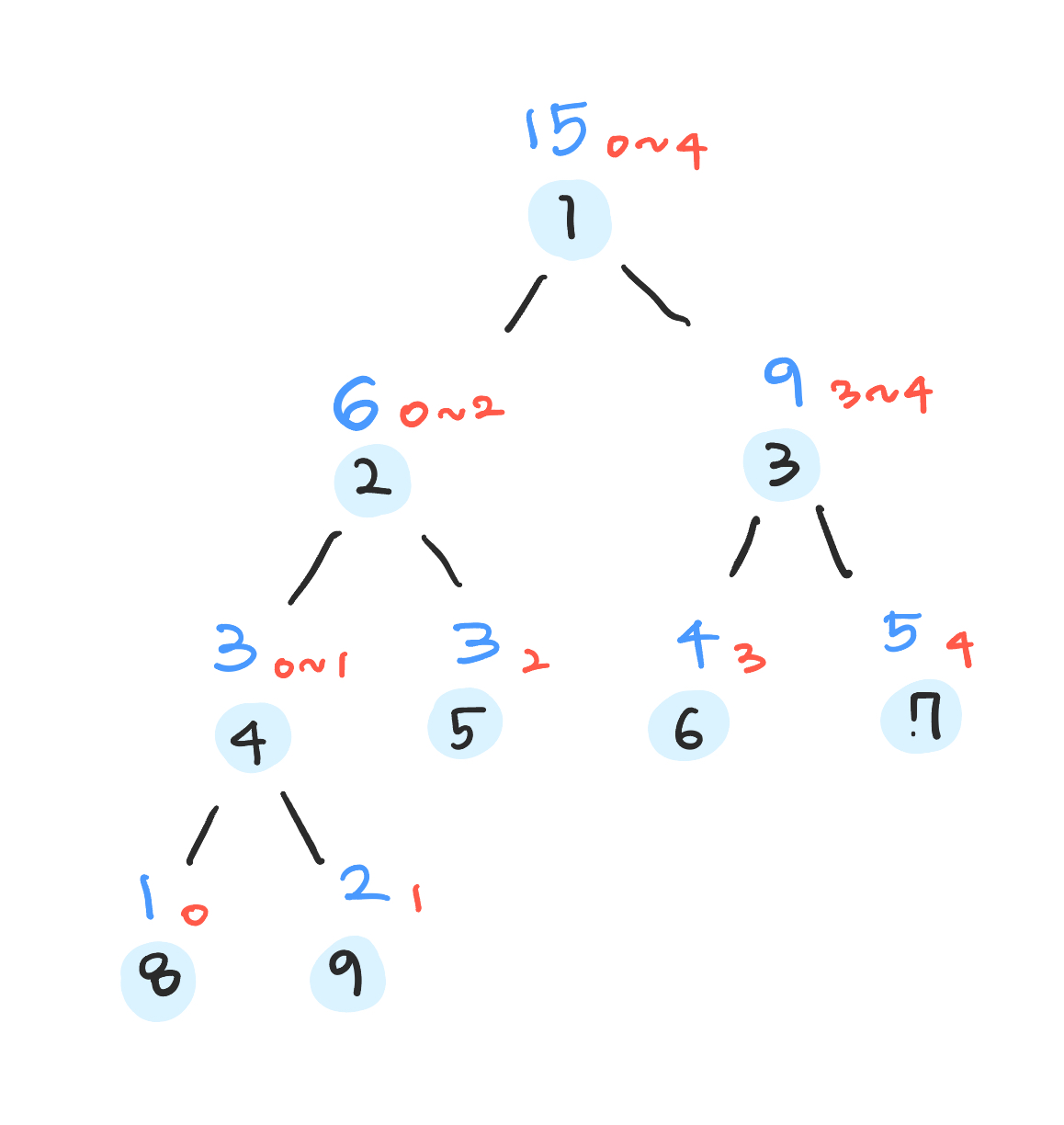
합을 찾는 과정을 코드로 구현하기
이것도 재귀함수로 구해준다. 원하는 검색 값은 left, right이다. start, end, node는 재귀함수를 위한 시작 값이다.
func getSum(_ start: Int, _ end: Int, _ node: Int, _ left: Int, _ right: Int) -> Int {
if right < start || left > end {
return 0
}
if left <= start && right >= end { // 검색하는 값이 start...end 범위안에 들어간다면
return tree[node]
}
let mid = (start + end) / 2
let leftChild = getSum(start, mid, node * 2, left, right)
let rightChild = getSum(mid + 1, end, node * 2 + 1, left, right)
return leftChild + rightChild
}
print(getSum(0, N-1, 1, 2, 4)) // 0..<N, node 1부터 시작
값 업데이트 하기
여기서 Segment Tree의 묘미는 값을 쉽게 업데이트할 수 있다는 것이다. 만약에 [1, 2, 3, 4, 5] 배열로 Segment Tree를 만들었는데 index 2의 3을 5로 만들고 싶다면? index 2를 포함하고 있는 모든 노드에 +2를 해주면 된다.
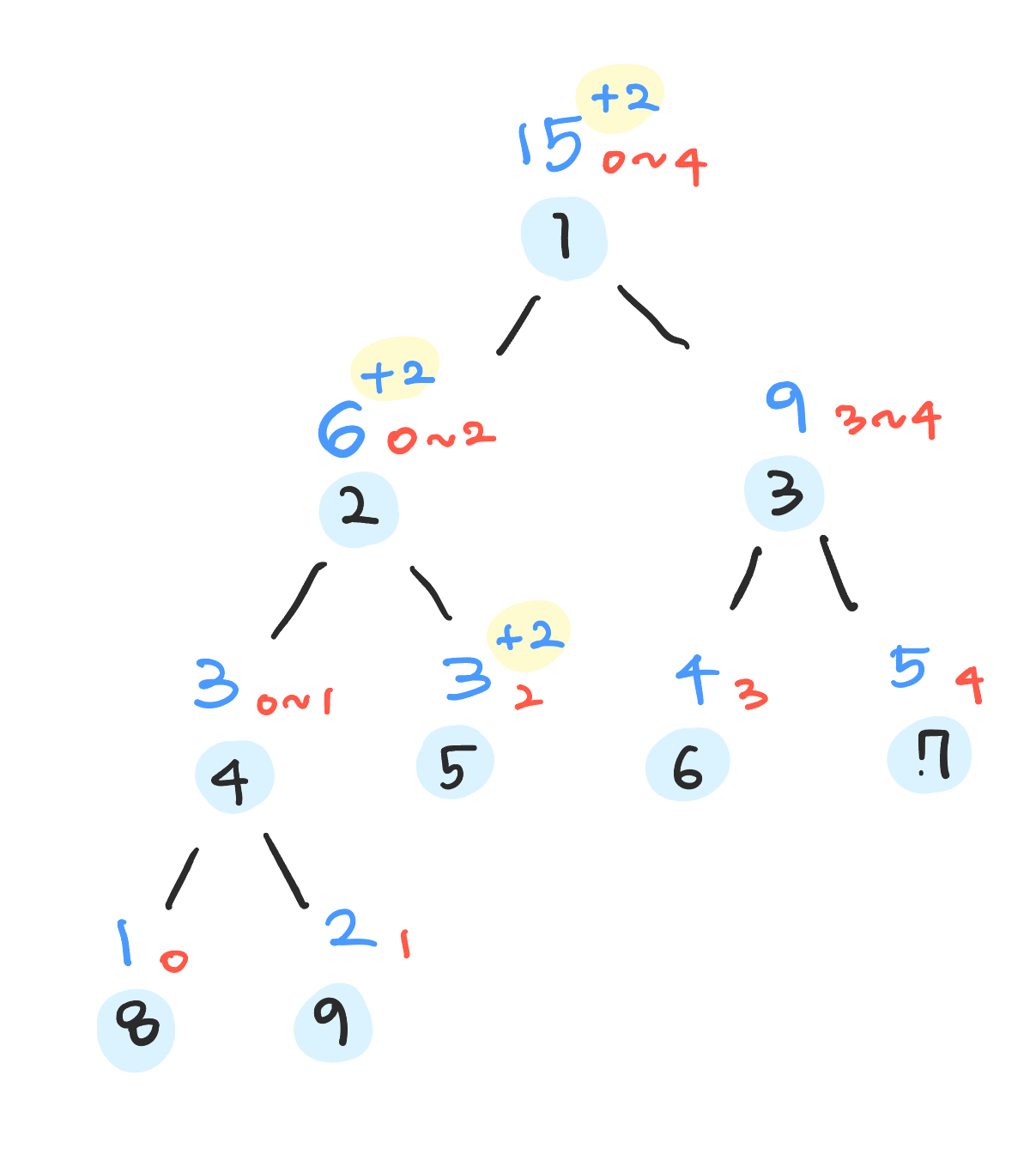
func update(_ start: Int, _ end: Int, _ node: Int, _ index: Int, _ value: Int) {
if index < start || index > end { return } // 범위 바깥이면 return
tree[node] += value // 노드에 value 를 더해준다.
if start == end { return } // 마지막 Leaf 노드일 경우 return
let mid = (start + end) / 2
update(start, mid, node * 2, index, value)
update(mid + 1, end, node * 2 + 1, index, value)
}
update(0, N-1, 2, 2) // value 를 더하는 것이니 2를 넣어준다
print(tree) // [0, 17, 8, 9, 3, 5, 4, 5, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
마치며
자료구조를 공부해 보면 볼수록 뭔가 생각보다 단순하고, 어렵지 않고 합리적이라는 것을 느낄 수 있었다. 알고리즘을 공부할수록 사람들이 많이 고민했구나... 세상에 천재들이 너무 많구나... 계속 느끼게 되는 것 같다.
이 글을 이해했다면...? 골드 1의 두 문제를 손쉽게? 풀 수 있다. 물론 2357번의 경우 조금의 응용이 필요하지만...
'→ 알고리즘 관련' 카테고리의 다른 글
| [Algorithm] Bitmask (비트마스크) (Swift) (0) | 2024.07.02 |
|---|---|
| [Algorithm] 고차함수 정리(Swift) (0) | 2024.06.28 |
| [Algorithm] Union-Find 알고리즘 (Swift) (0) | 2024.06.19 |
| [Algorithm] 큐 구현하기 (Swift) (2) | 2024.06.13 |
| [Algorithm] Swift로 구현해보는 정렬 알고리즘1 (버블, 선택, 병합 정렬) (0) | 2024.04.11 |