알고리즘의 기본이라고 할 수 있는 정렬. 개념은 알고 있었으나 한 번씩 구현해보고 싶었다. 우선 가장 쉬운 정렬 알고리즘부터 시작해 보려 한다.
버블 정렬
물론 시간복잡도가 O(n^2)으로 정렬 중에 가장 정직하고 비효율적인 알고리즘이다. 계속 바로뒤의 값과 비교하면서 크기를 비교하면서 위치를 바꿔주면 된다. 아래의 gif가 가장 쉽게 표현한 것 같아서 가져왔다.

버블 정렬 구현하기
맨 마지막으로 가는 숫자는 가장 큰 숫자가 되므로 제외하고 다음 정렬을 수행한다.
func bubbleSort(_ array: [Int]) -> [Int] {
var array = array
for i in 0..<array.count-1 {
for j in 0..<array.count-i-1 {
if array[j] > array[j+1] {
array.swapAt(j, j+1)
}
}
}
return array
}
버블 정렬 업그레이드
잘 정렬되어 있더라도 위의 알고리즘은 모든 정렬을 순회한다. 만약 정렬되어 있는 경우에는 swapAt이 작동하지 않을 것이다. 아래와 같이 isSwap변수를 두어 이것을 통해 정렬 종료여부를 판단한다. 시간복잡도는 변함이 없지만 분명 효율적으로 변하였다.
func bubbleSort(_ array: [Int]) -> [Int] {
var array = array
for i in 0..<array.count-1 {
var isSwap = false
for j in 0..<array.count-i-1 {
if array[j] > array[j+1] {
array.swapAt(j, j+1)
isSwap = true
}
}
if !isSwap {
break
}
}
return array
}
선택 정렬
아래처럼 배열 앞에서부터 쭉 뒤로 비교하면서 가장 작은 값을 찾아 바꿔주는 방법이다.

선택 정렬 구현
아래와 같이 가장 작은 값의 index를 저장한 후 앞에서부터 바꾸어 나가면 된다.
func selectionSort(_ array: [Int]) -> [Int] {
var array = array
for i in 0..<array.count {
var k = i
for j in i..<array.count {
if array[k] > array[j] {
k = j
}
}
array.swapAt(i, k)
}
return array
}
병합 정렬
위의 버블 정렬, 선택 정렬은 시간복잡도가 O(n^2)인데 반해, 병합 정렬은 O(nlogn)으로 더 효율적인 정렬방법이다. 왜냐하면 n번을 순회하지만 단계자체는 logn단계로 이루어졌기 때문에 자료의 수가 많을 때, 가장 효율적인 알고리즘이다. 반으로 나누고 나눠서 양쪽 두 배열을 병합하는 알고리즘이다.
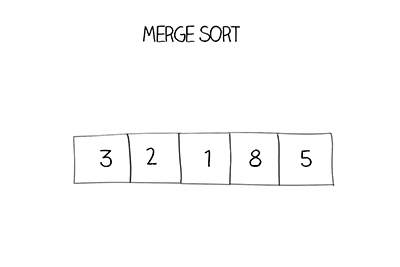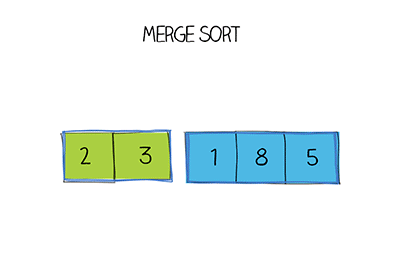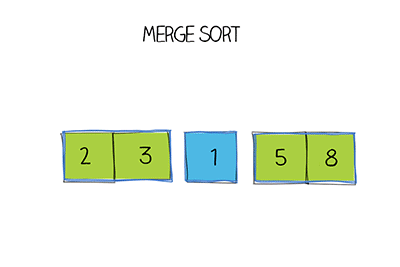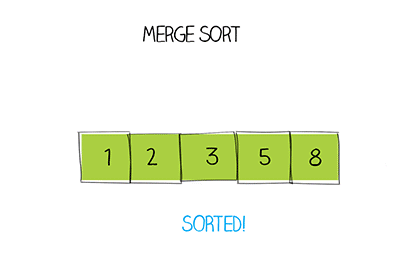
병합 정렬 구현
병합 정렬의 경우 특징은 잘게 쪼개서 병합하는 과정을 계속 반복하는 것인데, 여기서 재귀함수를 사용하여 구할 수 있다. 아래의 로직이 계속 반복된다고 할 수 있다.
if only one item
return
else
Sort left half of items
Sort right half of items
Merge sorted halves
이를 코드로 표현하면... 아래와 같다. 항상 재귀함수는 구현할 때마다 재밌는 것 같다.
func mergeSort(_ array: [Int]) -> [Int] {
if array.count == 1 { return array }
let n = array.count/2
let left = Array(array[0..<n])
let right = Array(array[n...])
func merge(_ left: [Int], _ right: [Int]) -> [Int] {
var merged = [Int]()
var left = left
var right = right
while !left.isEmpty && !right.isEmpty {
if left[0] < right[0] {
merged.append(left.removeFirst())
} else {
merged.append(right.removeFirst())
}
}
return merged + left + right
}
return merge(mergeSort(left), mergeSort(right))
}'→ 알고리즘 관련' 카테고리의 다른 글
| [Algorithm] Union-Find 알고리즘 (Swift) (0) | 2024.06.19 |
|---|---|
| [Algorithm] 큐 구현하기 (Swift) (2) | 2024.06.13 |
| [Algorithm] 이진탐색 (Binary Search) (Swift) (0) | 2024.04.08 |
| [Algorithm] 자료구조 - Swift와 알아보는 자료구조의 종류 (0) | 2024.04.02 |
| [Algorithm] 시간복잡도에 대해서 (big-O, Ω, θ 표기법) (2) | 2024.03.26 |