문제 소개
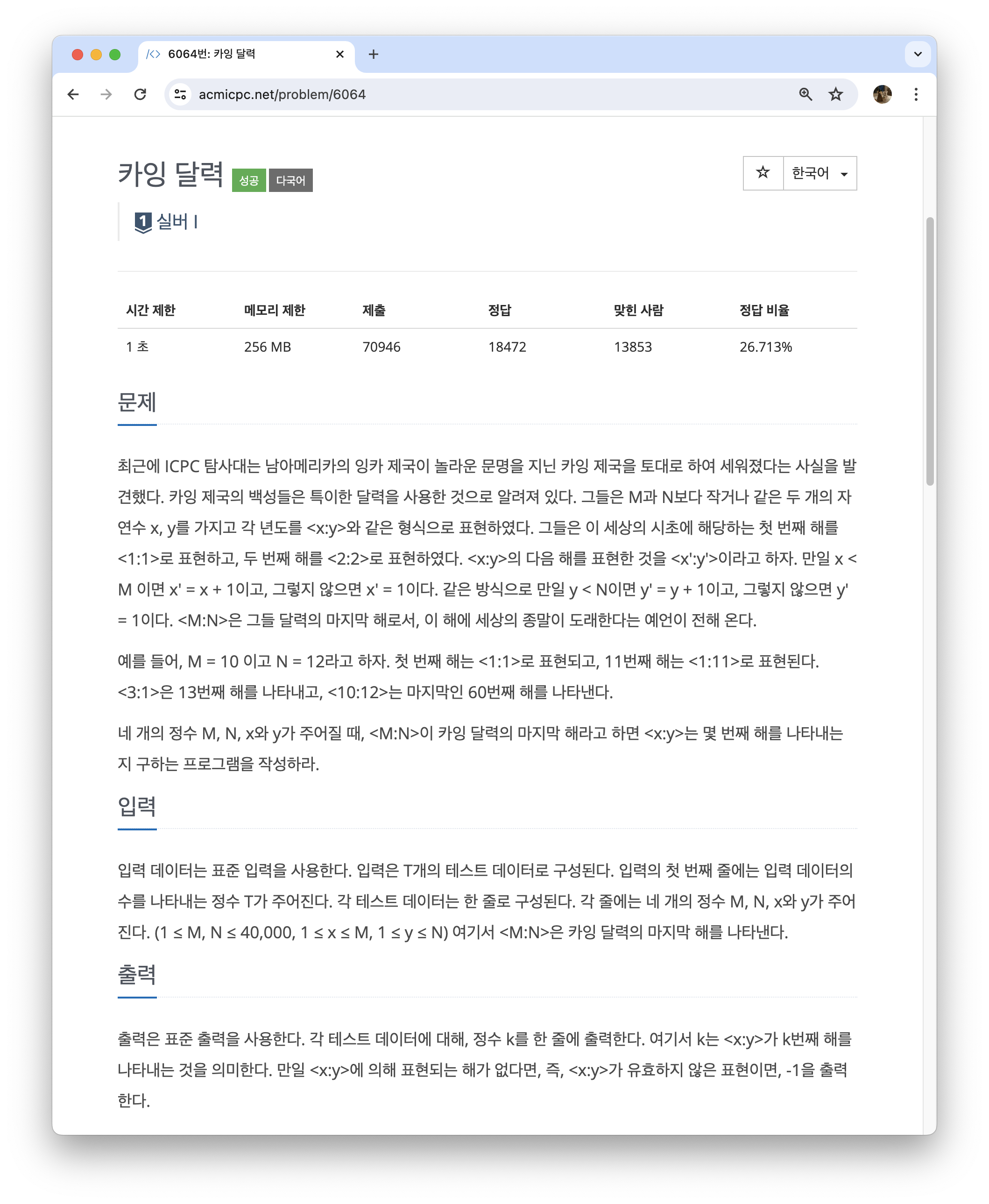
6064번: 카잉 달력
입력 데이터는 표준 입력을 사용한다. 입력은 T개의 테스트 데이터로 구성된다. 입력의 첫 번째 줄에는 입력 데이터의 수를 나타내는 정수 T가 주어진다. 각 테스트 데이터는 한 줄로 구성된다.
www.acmicpc.net
진법과 아주 비슷한 개념인데 진법은 위로 쌓아가지만 위의 카잉 달력은 해당 숫자가 넘으면 다시 1로 시작한다는 차이점이 있다.
풀이 방법
m, n, x, y가 주어지는데 아래와 같이 볼 수 있다. 결국 a와 b를 구하라는 뜻인데, 단순하게 a를 0부터 차례로 대입해나가면 된다. 그리고 최대 연도(종말 연도)는 m과 n의 최소공배수로 볼 수 있다.
year % m = x
year % n = y
year = ma + x
year = nb + y
내가 작성한 코드는 아래와 같다. 사실 m과 n중 최댓값을 찾아서 더해나가면 좀더 빠르겠지만... 그러면 코드가 길어져서 그냥 m을 기준으로 두고 작성했다.
import Foundation
let n = Int(readLine()!)!
func gcd(_ a: Int, _ b: Int) -> Int {
return b == 0 ? a : gcd(b, a % b)
}
func lcm(_ a: Int, _ b: Int) -> Int {
return a * b / gcd(a, b)
}
func kaing(_ m: Int, _ n: Int, _ x: Int, _ y: Int) -> Int {
var year = x
while year <= lcm(m, n) {
if year % n == 0 {
if y == n { return year }
}
if year % n == y { return year }
year += m
}
return -1
}
for _ in 0..<n {
let mnxy = readLine()!.split(separator: " ").map { Int($0)! }
let (m, n, x, y) = (mnxy[0], mnxy[1], mnxy[2], mnxy[3])
print(kaing(m, n, x, y))
}
속도는 0.068초로 아주 문제없는듯 하다.

'→ Problems' 카테고리의 다른 글
| [Algorithm] 백준 - 13023번 ABCDE (Swift) (0) | 2024.05.10 |
|---|---|
| [Algorithm] 백준 - 나무 자르기 (이분탐색) (0) | 2024.05.02 |
| [Algorithm] 백준 - 2156번 포도주 시식 (Swift) (1) | 2024.04.18 |
| [Algorithm] 백준 - 1929번 소수구하기 (Swift) (에라토스테네스의 체) (1) | 2024.04.14 |
| [Algorithm] 백준 - 1918번 후위표기식 (postfix) (0) | 2024.04.14 |