⚙️ 벨먼 포드 (Bellman-Ford) 알고리즘
최단거리를 구할 수 있는 아름다운? 알고리즘이다. 이런 알고리즘은 일단 코드로 보고 어떻게 돌아가는지 아는 게 중요하다고 생각해서 바로 Pseudo code를 가져와 봤다. 위키백과 영어버전에서 가져왔다.
function BellmanFord(list vertices, list edges, vertex source) is
distance := list of size n
// Step 1: initialize graph
for each vertex v in vertices do
distance[v] := inf
// The distance from the source to itself is zero
distance[source] := 0
// Step 2: relax edges repeatedly
repeat |V|−1 times:
for each edge (u, v) with weight w in edges do
if distance[u] + w < distance[v] then
distance[v] := distance[u] + w
실제 의사코드에는 최적의 경로를 저장하는 predecessor가 있지만 이것은 제외하고, 위의 두 스탭만 알면 일단 최단거리는 구할 수 있다.
🦜 Swift로 구현해 보기 (초급 버전) - 최단 거리 구하기
Edge라는 간선을 나타내는 구조체가 있다고 해보자. 그렇게 된다면 아래와 같이 입력된 간선들을 정점-1 만큼 반복해서 distance를 업데이트시켜 주면 된다.
struct Edge {
var from: Int
var to: Int
var weight: Int
}
func bellmanford(v: Int, edges: [Edge], start: Int) -> [Int] {
var distance = Array(repeating: Int.max / 2, count: v)
distance[start] = 0
for _ in 0..<v-1 {
for edge in edges {
distance[edge.to] = min(distance[edge.to], distance[edge.from] + edge.weight)
}
}
return distance
}
아래와 같이 내가 만든 수제 그래프에 대입해보자.

let edges = [
Edge(from: 0, to: 1, weight: 3),
Edge(from: 0, to: 2, weight: 5),
Edge(from: 1, to: 2, weight: 1),
Edge(from: 1, to: 3, weight: 1),
Edge(from: 2, to: 3, weight: 2)
]
print(bellmanford(v: 4, edges: edges, start: 0)) /// [0, 3, 4, 4]
어째서 이렇게 간단하게 해결되는 거지? 단순히 v-1번 간선을 반복하니까 최소경로가 나오네...? 🤔 라는게 내 생각이었다. 뭔가 신기하지 않은가? 그냥 간선정보 여러 번 돌리니까 답이 나와버린다? 직관적으로 와닿지 않았던 것 같다.
🕸️ 벨먼 포드 알고리즘 원리
원리는 최단경로의 최대 간선은 v-1, Relaxation(완화 연산)에 있다고 한다.
🚧 최단 경로의 최대 간선은 v-1
여기서 v는 vertex의 개수를 이야기한다. 최단 경로는 최대 v-1개의 간선을 지난다. 그 이상을 지나면 최소시간으로 갈 수가 없다. (이 상황에서 음수 사이클은 제외하고 생각해 보자) 한 간선을 여러 번 지나면 무조건 낭비다.
🧙 Relaxation
사실 완화연산도 뭔 소리야? 할지 모른다. 현재까지 알려진 최단 경로를 반복적으로 업데이트시켜 준다고 생각하면 된다. v-1 반복의 의미는 1번째 반복에서는 1개의 간선을 지날 때의 최단 경로, 2번째 반복에서는 2개의 간선을 지날 때의 최단 경로, 3번째 반복에서는 3개의 간선을 지날 때의 최단 경로를 업데이트시켜 주는 것이다.
🕊️ Swift로 구현해 보기 (중.. 급?) - 경로도 같이 구해보기
위를 이해했다면 최단거리까지의 경로도 확인해 볼 수 있는 predecessor도 출력해 볼 수 있다. predecessor는 최단 경로로 가기까지 이전 경로를 이야기한다.

예를 들면, 나온 결과가 [-1, 0, 1, 1]이라면 1에 도착하는 최단경로는 0을 통해서 가야 하고, 2에 도착하는 최단경로는 1을 통해 가야 하고, 3에 도착하는 최단 경로는 1을 통해서 가야 한다는 뜻이다. (-1은 갈 곳이 없다는 뜻으로 내가 지정했다)
func bellmanford(v: Int, edges: [Edge], start: Int) -> (distance: [Int], predecessor:[Int]) {
var distance = Array(repeating: Int.max / 2, count: v)
var predecessor = Array(repeating: -1, count: v)
distance[start] = 0
for _ in 0..<v-1 {
for edge in edges {
if distance[edge.from] + edge.weight < distance[edge.to] {
distance[edge.to] = distance[edge.from] + edge.weight
predecessor[edge.to] = edge.from
}
}
}
return (distance, predecessor)
}
let edges = [
Edge(from: 0, to: 1, weight: 3),
Edge(from: 0, to: 2, weight: 5),
Edge(from: 1, to: 2, weight: 1),
Edge(from: 1, to: 3, weight: 1),
Edge(from: 2, to: 3, weight: 2)
]
bellmanford(v: 4, edges: edges, start: 0)
/// predecessor: [-1, 0, 1, 1]
/// distance: [0, 3, 4, 4]
👽 음의 가중치?
흔히 다익스트라, 벨먼 포드 알고리즘의 가장 큰 차이점은 벨먼 포드는 음의 가중치도 가능하다는 점을 많이 든다.
🥸 다익스트라와 음의 가중치
하지만 원리를 이해하면 다익스트라도 음의 가중치가 있어도 계산이 되긴 된다. 아래와 같은 간단한 그래프가 있다고 해보자.

아래가 다익스트라 알고리즘을 했을 때이다. 동그라미는 방문 체크이다.
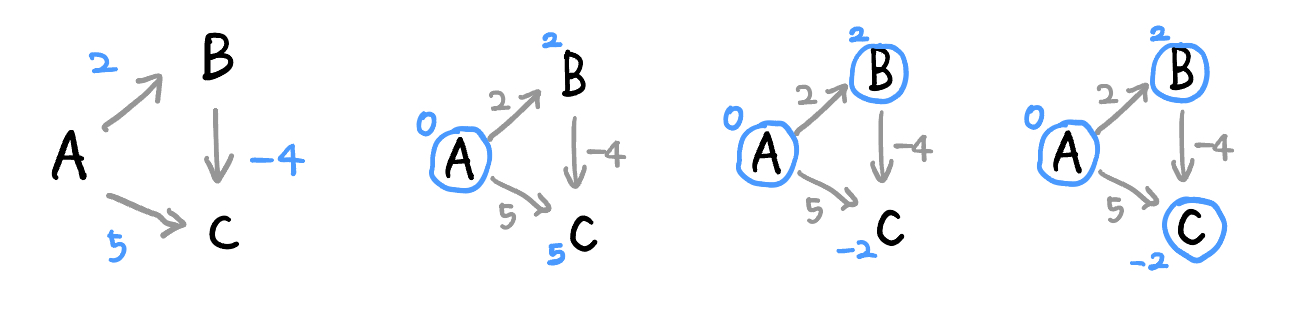
잘 계산이 된다. 하지만 아래의 그래프를 봐보자.

아래와 같이 이미 가장 짧았던(?) B는 방문처리를 해버렸으므로 1로 업데이트가 안된다!!!

결국 다익스트라는 음의 가중치가 있다면 그 경로가 최적인지 보장할 수 없다... 결국 음의 가중치가 있을 땐 다익스트라를 쓰면 구한 값이 최적의 정답은 아니다.
🥸 벨먼 포드의 음의 가중치
벨먼포드는 방문처리 그런 거 없다. v-1번 무지성 갱신을 해주기 때문에 음의 가중치도 잘 잡아준다.
let edges = [
Edge(from: 0, to: 1, weight: 2),
Edge(from: 0, to: 2, weight: 5),
Edge(from: 2, to: 1, weight: -4)
]
bellmanford(v: 3, edges: edges, start: 0)
/// predecessor: [-1, 2, 0]
/// distance: [0, 1, 5]
하지만 여기서 벨먼 포드는 시간복잡도가 O(VE)이고, 다익스트라는 O(VlogV + ElogV)이다. (우선순위 큐를 쓸 경우) 결국 시간복잡도는 log를 안 붙인 벨먼 포드가 높을 수밖에 없는데, 잘 선택을 해서 방식을 결정하면 될 것 같다고 생각했다.
👽 음의 사이클
벨만 포드는 음의 사이클을 추적할 수 있다! 왜냐하면 계속 사이클을 돌리면서 갱신해 줄 수 있기 때문! 아래와 같은 음의 사이클이 있다고 해보자. 최단거리는 -∞ 라고 할 수 있다. 한 바퀴 돌 때마다 최단거리가 -1씩 줄어들기 때문...
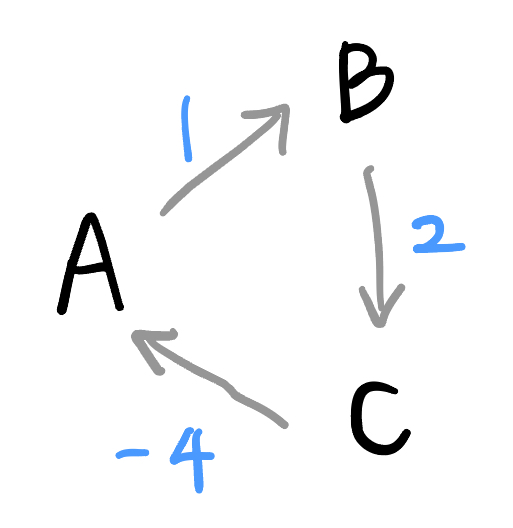
이걸 벨만 포드로 어떻게 확인할 수 있을까? 바로 사이클을 한번 더 돌려보는 것이다.
func bellmanford(v: Int, edges: [Edge], start: Int) -> (distance: [Int], predecessor:[Int]) {
var distance = Array(repeating: Int.max / 2, count: v)
var predecessor = Array(repeating: -1, count: v)
distance[start] = 0
for _ in 0..<v-1 {
for edge in edges {
if distance[edge.from] + edge.weight < distance[edge.to] {
distance[edge.to] = distance[edge.from] + edge.weight
predecessor[edge.to] = edge.from
}
}
}
for edge in edges {
if distance[edge.from] + edge.weight < distance[edge.to] {
print("음의 사이클!")
}
}
return (distance, predecessor)
}이렇게 작성하면 아래와 같이 출력된다!
let edges = [
Edge(from: 0, to: 1, weight: 1),
Edge(from: 1, to: 2, weight: 2),
Edge(from: 2, to: 0, weight: -4)
]
bellmanford(v: 3, edges: edges, start: 0)
// 음의 사이클!하지만 아래와 같은 모양새는 음의 사이클이 아니다. 한바퀴 도는 것이 무조건 손해이기 때문! 아래의 경우는 잘 계산된다.

'→ 알고리즘 관련' 카테고리의 다른 글
| [Algorithm] KMP 알고리즘 (문자열 검색) (0) | 2025.05.05 |
|---|---|
| [Algorithm] 플로이드 워셜 알고리즘 (1) | 2025.02.08 |
| [Algorithm] 다익스트라 알고리즘 (0) | 2025.02.08 |
| [Algorithm] 0-1 배낭문제(Knapsack Problem) - 백트래킹 (0) | 2025.02.07 |
| [Algorithm] 0-1 배낭문제(Knapsack Problem) - DP (0) | 2025.02.07 |